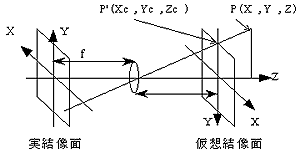
図1 透視投影
2.3次元形状の生成
2.1 ステレオ法による3次元形状の入力
伝統工芸品の新しい形状を生成するために,既存の製品の形状をステレオ法により入力する方法と断面形状の定義により回転体形状を生成する2つの方法を開発した。特に,前者の方法である多方向からのカメラにより,既存の製品を高精度に形状入力する手法について述べる。
2.1.1 カメラパラメータの算出
本手法では,ステレオ法の対応点検出の困難を避けるために,レーザのスリット光を物体に照射し,対応点を検出しやすいよう工夫した。この時,周囲の光環境を安定にするために暗幕を用いた。
 図1 透視投影 |
三角測量の原理により,3D空間の一点は,カメラの視線がなす2直線の交点として一意に決定できる。図1で示すように,空間中のある一点P(X,Y,Z)をカメラの仮想結像面へ透視した点P'(Xc,Yc,Zc),すなわち,測定点Pへ向かっている視線と結像面との交点は,次のように与えられる。

ここで,fはレンズの焦点距離である。
図1の透視変換は,点Pと点P'がともにカメラに固定した座標系で表現したとき適用できる。しかし,通常はカメラ座標系と物体座標系とに分離した座標系を用いる方が便利である。カメラ座標系で結像面(Zc=0)における座標(Xc,Yc)は,次になる。
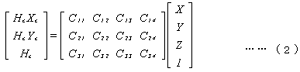
ここでHc=(Z+f)/fである。
この3×4のC行列がカメラパラメータであり,カメラの位置,姿勢,画角などの情報が含まれている。式(2)の行列式を展開すると次の2式が得られる。
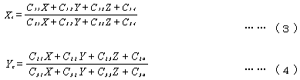
式(3)と式(4)に,物体座標系で基準となる点(X,Y,Z)とそれに対応するカメラ結像面での位置(Xc,Yc)を代入し2つの連立方程式を作る。したがって,カメラパラメータのC11からC34までの12個の未知数を求めるには,同一平面上にない6個の基準点が必要になる。
2.1.2 対応点の決定と3次元位置の算出
ステレオ法で一番重要なことは,物体上の3D位置P(X,Y,Z)が,左右のカメラのどこに写っているかを検出することである。図2は,左右のカメラで観察したスリット光像を,画像処理により2値化,細線化したものを,さらに分割し対応点を求めた図である。

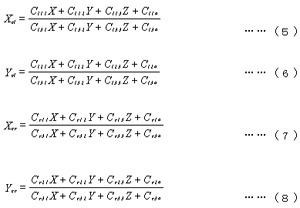
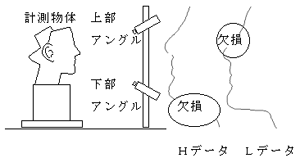 図3 垂直方向のデータ補間 |
(2)水平方向のデータ補間
水平方向に関しては,通常左右のカメラの対応点検出により,3D座標を算出する。しかし,図4のように物体表面の凹凸の状態に起因して,一方のカメラでしかスリット光が撮像できない場合があり,そのためにデータの欠損が生じる。
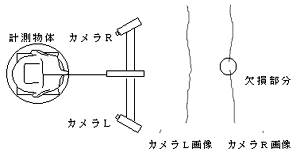 図4 水平方向のオクルージョンの発生 |
これを改善するためにスリット光とカメラ1台の対で3D座標を求める。物体に射するスリット光平面は,Y-Z平面に等しいのでX座標値を0と置くことができる。従って,カメラLの場合は式(5),(6)を連立させ,またカメラRの場合は式(7),(8)連立させることによって3D座標(Y,Z座標)を求めることができる。これらの3D座標を用いた左右のデータの補間は,垂直方向のデータ補間方法と同様である。図5頭部の石膏モデル
に示す人間頭部モデルの3D計測結果を図6補正を行なった人間頭部の計測データに示す。また,図73D形状入力施策装置に今回開発した3次元形状入力装置の外観を示す。
|
|
|
|