平成10年度研究報告 VOL.48
パルスレーザによる材料プロセッシング技術の研究 |
|
 |
2.2 各パラメータのフィッテイング
前節では,熱伝導方程式の骨格となる熱の収支について述べた。温度プロファイルやその時間変化は,熱伝導方程式中の比熱等の各パラメータに依存する。これらのパラメータは,式(1)の熱伝導度κ(T)のように一般的には温度の関数となっている。シミュレーションでは,温度依存性の比較的小さい比熱cや密度ρ等は定数として扱い,温度依存性の大きな熱伝導度κ(T)及び蒸気圧P(T)を適当な関数でフィッテイングした値を用いた。本節では,文献より得た測定データをフィッテイングした結果について述べる。なお,より高精度なシミュレーションのためには,各パラメータのより詳細なデータが必要である。そのため,これらのデータが比較的整っているSiをモデル材料として扱うことにした。
2.2.1 熱伝導度のフィッティング
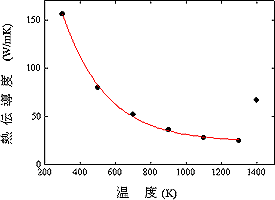
熱伝導度κ(T)のデータ及びフィッテイング結果を図5に示す。用いた関数は実験式で,調べた範囲で最も良く適合した関数である。図5から,
κ(T) = 0.235 + 4.45 exp ( - T / 247 ) (8)
とした。なお,図中で1400K付近でデータに飛びがあるのは,融点を超えた温度における点のため液相となったためである。液相における熱伝導度は一定値とした。
2.2.2 蒸気圧のフィッティング
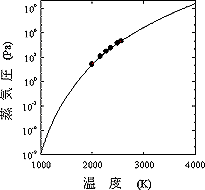
蒸気圧P(T)のデータおよびフィッティング結果を図6に示す。関数は実験式である7)。図6から,
| |
- 8.98×103/ T - 50.4 + 17.3 log(T) (9) |
| P(T) = 10 |
|
とした。
 |
 |
| 図5 熱伝導度の温度依存性 |
図6 蒸気圧の温度依存性 |
表1 シミュレーションに用いたパラメータ
| 吸収係数 |
1.6×108[/m] 密度 2.33[kg/m3] |
| 反射率 |
固体0.68 液体0.7 |
| 融解熱 |
1.8×106[J/kg] 比熱 0.702[J/(kgK)] |
| 熱伝導率 |
固体 0.235+4.45 exp(-T/247) [W/(mK)] |
| 液体 0.67[W/(mK)] |
| 蒸気圧 |
logP=-8.98×103/T-50.4+17.3 log(T) [Pa] |
|
2.3 温度分布シミュレーション結果及び考察
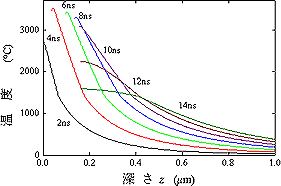
シミュレーションに用いたパラメータを表に示す。図7にレーザ照射が40 kJ/m2の場合の温度プロファイルの2 ns毎の時間変化を示した。横軸は深さを表し,左側が材料表面方向である。表面でプロットが無い部分は,材料表面が蒸発することにより消失し,表面が後退していることを表している。温度プロファイルの変曲点は,融点を通過する際の潜熱や熱伝導の不連続によるものである。温度プロファイルは,主に光の吸収に依存した形状となっているように思われ,時間が経過すると熱伝導により深い部分に熱が移動している。
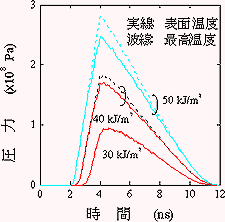
表面温度が高い場合には,最表面では,内部に比べわずかに温度が下がっている。これは,蒸発により表面で気化熱が奪われたためであると考えられるが,この温度降下は小さい。この温度差による内部圧力を抑えきれなくなることで爆発が起き,液的状粒子が生成するという提案が行われている8)。そこで,これらの温度に相当する蒸気圧の時間変化を調べることにした。図8にフルエンスを変化させた場合の表面と最高温度点に対する蒸気圧の時間変化を示す。ここで,表面直上では蒸発粒子が高密度に存在するため,蒸気圧はリコイル圧と等しいと考えて良いであろう。そうすると,図8の表面と内部の最高温度点における圧力差は,材料の表面を抑える力と内部圧力との差を表すことになり,フルエンスが40
kJ/m2の場合には,最大で10 MPaもの圧力差が生じることがわかった。また,図7から,レーザ光照射時間内での熱拡散長は1 μm以下であると考えられ,レーザ光照射領域(数100
μm)に比べ十分小さい。以上から,図9の模式図に示すように材料表面の液相の挙動やこれに関連して働く力として以下のものが考えられる。
(1)内部と表面との圧力差を支えるための液相の粘性や表面張力。
(2)レーザ光の不均一のために生じる内部圧力差を解消しようとする面内方向の外側に向かう力。
(3)リコイル圧(表面の蒸気圧)の面内方向の不均一のため,周囲が押し出される力。
ここで,(1)の表面張力の時間変化を計算し,曲率を求めた。曲率ρST,表面張力σの計算には次の式を用いた9)。
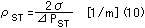
σ= 727 - 0.104 ( T - 1683) ×10-3 [N/m]
ここで, PSTは内部と外部の圧力差である。図10にレーザフルエンスが40 kJ/m2の場合の曲率の時間変化を示した。このフルエンスでは,曲率半径が最小で約10
μmとなった。この値はレーザ照射径(数100 μm)に比べ小さいことから,圧力差を表面張力では支えられないことになる。以上から,表面張力のみによる効果を考慮すると,ある時間で表面張力は破綻し,爆発等の現象が起こりうること考えられる。このことにより,表面表面性状が変化したり,液的状粒子が生成される可能性がある。
PSTは内部と外部の圧力差である。図10にレーザフルエンスが40 kJ/m2の場合の曲率の時間変化を示した。このフルエンスでは,曲率半径が最小で約10
μmとなった。この値はレーザ照射径(数100 μm)に比べ小さいことから,圧力差を表面張力では支えられないことになる。以上から,表面張力のみによる効果を考慮すると,ある時間で表面張力は破綻し,爆発等の現象が起こりうること考えられる。このことにより,表面表面性状が変化したり,液的状粒子が生成される可能性がある。
(2)と(3)の力は,レーザ光照射領域の中心から外側に向かって働く力で,外側にある物質を押し出すことになる。この力は,上述の通りレーザフルエンスが40 kJ/m2の場合には最大で約10
MPaという大きな力を生じるため,液相の物質が移動したりして,表面の表面性状変化や液的状粒子の生成の可能性がある。
以上の考察から,(1),(2),(3)のいずれの効果でも,ある程度大きなフルエンス照射による表面表面性状の変化や液的状粒子生成が説明され得ることが明らかになった。しかし,(1)に対して(2),(3)の液相物質の移動方向が逆であることから,これらが競合することが考えられ,実際の挙動はさらに複雑であることが予想される。
 |
 |
| 図7 温度プロファイルの時間経過による変化 |
図8 圧力の時間変化(フルエンス依存性) |
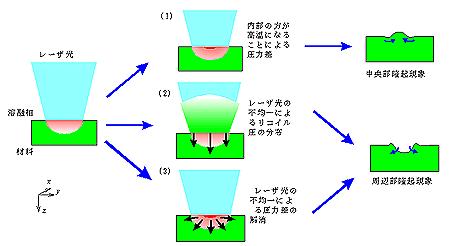 |
| 図9 材料表面に働く力の模式図 |
3.結言
パルスレーザ光を材料表面に照射した際の,温度プロファイルの変化を差分法によりシミュレーションを行った。その結果,材料表面近傍での急速な温度上昇により,大きなリコイル圧を受けることや,気化熱により材料表面より材料内部で温度が高くなり圧力が上昇することから,液相領域に次の力の作用することが。明らかになった
(1)内部と表面との圧力差を支えるための液相の粘性や表面張力
(2)レーザ光の不均一のために生じる内部圧力差を解消しようとするxy面方向の外側に向かう力
(3)リコイル圧(表面の蒸気圧)のxy面内の不均一のため,周囲が押し出される力
PLAにより起こる材料表面の表面性状の変化や液的状粒子の生成が説明できることを示した。この結果を利用して,表面性状変化の抑制を図りたい。
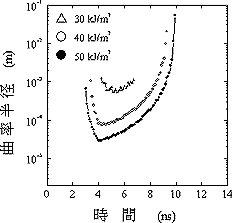 |
図10 表面張力による曲率半径の時間変化
(フルエンス依存性) |
|
謝辞
本研究の遂行に当たり,有益なご助言を頂いた金沢大学工学部電気・情報工学科の清水立生教授,森本章治助教授に感謝します。
参考文献
1)Y.F.Lu, S.Komuro and Y.Aoyagi:Laser-Induced Removal of Fingerprints from
Glass and Quartz Surfaces, Jpn.J.Appl.Phys., Vol.33, p4691-4696(1994).
2)K. G. Watkins, J. H. Larson, D. C. Emmony, W. M. Steen: Proceedings of
the NATO Advanced Study Insitute on Laser Processing:Surface Treatment
and Film Deposition, Kluwer Academic Publishers, p.907(1995).
3)T .Minamikawa, M. Tazoe, K. Segawa, Y. Yonezawa, A. Morimoto and T.Shimizu:
Preparation of a-axis oriented YBa2Cu3Ox superconducting films on MgO substrate
with PrBa2Cu3Ox buffer layers, Physica C, vol.267,p330(1996).
4)Y. Yonezawa, K. Segawa, S. Katayama, T. Minamikawa, A.Morimoto and T.Shimizu:
Reduction of Droplet Formation by Reducing Target Etching Rate in Pulsed
Laser Ablation, Jpn.J.Appl.Phys.Lett., Vol.33, p.1178(1994).
5)Y.Yonezawa, T.Minamikawa, A.Morimoto and T.Shimizu: Removal of Surface
Oxides on Copper by Pulsed Laser Irradiation, Jpn.J.Appl.Phys., Vol.37,
p.4505(1998).
6)応用物理学会編: 応用物理ハンドブック, 丸善, P275.
7)日本真空株式会社編: 真空ハンドブック,P132.
8)S.Otsubo, T.Minamikawa, Y.Yonezawa, A.Morimoto and T.Shimizu: Jpn. J.
Appl. Phys. Lett., Vol.29, p.73(1990).
9)S.V.Lukin, V.I.Zhuchkov et al.: J. Less-Commom Metals, Vol.67, p399(1979).


![]()
![]() PSTは内部と外部の圧力差である。図10にレーザフルエンスが40 kJ/m2の場合の曲率の時間変化を示した。このフルエンスでは,曲率半径が最小で約10
μmとなった。この値はレーザ照射径(数100 μm)に比べ小さいことから,圧力差を表面張力では支えられないことになる。以上から,表面張力のみによる効果を考慮すると,ある時間で表面張力は破綻し,爆発等の現象が起こりうること考えられる。このことにより,表面表面性状が変化したり,液的状粒子が生成される可能性がある。
PSTは内部と外部の圧力差である。図10にレーザフルエンスが40 kJ/m2の場合の曲率の時間変化を示した。このフルエンスでは,曲率半径が最小で約10
μmとなった。この値はレーザ照射径(数100 μm)に比べ小さいことから,圧力差を表面張力では支えられないことになる。以上から,表面張力のみによる効果を考慮すると,ある時間で表面張力は破綻し,爆発等の現象が起こりうること考えられる。このことにより,表面表面性状が変化したり,液的状粒子が生成される可能性がある。

