技術ふれあいミレニアム2000発表会要旨集
電磁シールド効果の解析

機械電子部 ○吉村　慶之　南川　俊治　筒口　善央
金沢大学工学部　長野　勇

１　目　的
　電子機器の高度化や無線通信機器の普及に伴い，不要電磁波が原因となる機器の誤動作が問題となっている。そこで，筐体に導電率の高い金属材料等を用いる方法や，プラスチック筐体に無電解メッキや導電性塗料を塗布することによって電磁波のシールドが行われている。最近ではペースメーカの誤動作対策のため，衣料に対してもシールド効果を持たせた製品開発が盛んに行われている。より有効に電磁波対策を行うためには，計算による解析によって電磁シールドの性質をよく把握しておくことが重要である。電磁波源から遠方距離におけるシールド効果は簡単な式により容易に求まるが，近傍距離においてはベクトル解析を伴うため複雑となる。しかし，電子機器の近くにおけるシールドは内部のプリント基板が電磁波源となるため，波源の近傍に対するシールド問題として取り扱う必要がある。ここでは，波源近傍のシールド効果を解析し，その性質について遠方における結果と比較検討することを目的とした。

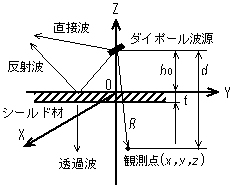
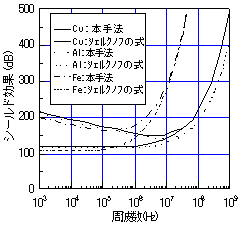
２　内　容
　シールド効果の解析は，材料の電気定数を理論式に導入することにより求められる。これは，製品の設計段階で効果の予測をたてることが可能であるため有効な手段である。ここでは，図１に示すような無限大平板のシールド材に対する解析を行った¹⁾²⁾。座標原点よりz=h₀の位置に電気ダイポール波源を設定し，波源と観測点との距離をRとする。ダイポール軸はシールド材に対して，水平（X）方向を想定する。シールド材上部では直接波と反射波があり，シールド板下部では下降波（透過波）のみが存在する。解析に際し，波源位置は固定し，観測点は任意位置に移動が可能とする。解析にあたり，表１に示す材料の電気定数を用い，厚みt=0.1mmとした。

2.1 周波数特性
　図１の解析モデルで観測点位置をｚ軸上とし，h₀=0.5m，ｄ=1mで，３種類の材料についてシールド効果の周波数特性を解析した。結果を図２に示す。また，シェルクノフの式より求まる遠方領域のシールド効果³⁾も同図に示す。ダイポール波源から観測点までの距離d=1mでは周波数が約48MHz以上において遠方領域(=波長/(2π))とみなせる。図２よりこの周波数領域以上において，本手法より求めた結果がシェルクノフの式から求めたシールド効果とよく一致しており，本手法の妥当性が検証できた。また，近傍領域でシールド効果を検討する場合，シェルクノフの式から求まる結果と異なることが確認できた。

図１解析モデル

表１　材料の電気定数

	ε_r	μ_r	σ(S/m)
Cu	1	1	5.81×10⁷
Al	1	1	3.64×10⁷
Fe	1	140	1.00×10⁷

ε_r:比誘電率　μ_r:比透磁率　σ:導電率

2.2 波源と観測点との距離
　Cu材を仮定し，波源と観測点との距離を変えた場合，図３に示すように距離が離れるに従いシールド効果は徐々に落ちていき，遠方領域となった時点で一定値となることがわかった。したがって，近傍領域でシールド効果を測定する場合，波源と観測点との距離が重要となる。また，遠方領域では波源と観測点との距離に依存せず，シールド効果は一意に定まることがわかった。


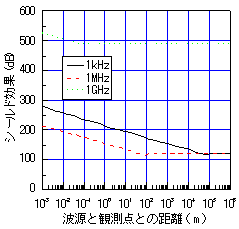図２シールド効果の周波数特性	図３波源と観測点位置によるシールド効果

３　結　果
　電子機器の電磁波による誤動作を防止するためには，シールドによる対策が必要不可欠である。そこで，理論解析によるシールド効果の各種性質を確かめた。その結果，以下のことがわかった。

(1)	電気ダイポール波源を考慮したシールド効果を解析的に求めた。その結果，遠方領域においてシェルクノフの式とよく一致しており，本手法の妥当性が確認できた。
(2)	近傍領域におけるシールド効果は一意には決まらず，観測点位置により異なるという結果が得られた。従って，材料の特性としてシールド効果を表現する場合は，観測点位置を明示しなければならないことがわかった。

謝　辞
　本研究はH10，11年度科学技術振興事業団のＲＳＰ事業（可能性試験）の一環として実施されたことを記し，関係各位に謝意を表します。
文　献

1)	長野勇:不均質媒質中の電磁波伝搬,朋友印刷(株),p.12-42(1997)
2)	吉村慶之,長野勇,横本広章,大浦利夫,八木谷聡:電気ダイポールの任意位置における多層媒質のシールド効果,信学技報,EMCJ99-127,p.105-112(2000)
3)	清水康敬,杉浦行:電磁妨害波の基本と対策,（社）電子情報通信学会,p.56-77(1995)

トップページ

2000要旨集