 チタンアルミの積層構造と弾性的性質
チタンアルミの積層構造と弾性的性質
化学食品部 田畑裕之
- 目的
次世代の軽量耐熱合金として研究開発が盛んなチタンアルミ金属間化合物は、二種類の相(物質)からなる層状組織粒(ラメラ)を形成する特徴がある。ラメラの積層構造と弾性的性質の関係を明らかにすることは、本合金開発の本質に関わる重要な問題である。前年度は、構成二相(六方晶のα2-Ti3Alと正方晶のγ-TiAl)のそれぞれの単結晶の弾性定数から任意の方向の結晶方位分布を計算、図示する方法を述べた。本報では、ラメラの積層構造に基づいて、構成二相の弾性的性質からラメラの巨視的な弾性的性質を帰納法的に見積もることを目的とする。
- 内容
2.1 ラメラの積層構造
1)Ti-46mol%Al PST結晶の組織
 ラメラの積層構造を調べる目的で、試料全体が一個のラメラからなる Ti-46mol%Al PST結晶(単結晶様の結晶)を育成した。図1にその電顕組織を示す。写真はラウエ法により方位を決定した上で、正確に積層面真横から撮影したものである。これより、白く明瞭に見える薄層部分がα2相で平均の厚さは0.3μmであった。その他の部分がγ相で、強く腐食したのでγ/γ界面も見受けられ、一枚のγ板の厚さは平均約 0.6μmであった。また、一枚のγ板の中には腐食の程度に差があるドメイン(微結晶)の存在が認められる。ドメインの積層面方向のサイズは不鮮明ながら、数μmから数十μmと推察される。
ラメラの積層構造を調べる目的で、試料全体が一個のラメラからなる Ti-46mol%Al PST結晶(単結晶様の結晶)を育成した。図1にその電顕組織を示す。写真はラウエ法により方位を決定した上で、正確に積層面真横から撮影したものである。これより、白く明瞭に見える薄層部分がα2相で平均の厚さは0.3μmであった。その他の部分がγ相で、強く腐食したのでγ/γ界面も見受けられ、一枚のγ板の厚さは平均約 0.6μmであった。また、一枚のγ板の中には腐食の程度に差があるドメイン(微結晶)の存在が認められる。ドメインの積層面方向のサイズは不鮮明ながら、数μmから数十μmと推察される。
2)α2相とγ相およびγ相中のドメイン相互の方位関係
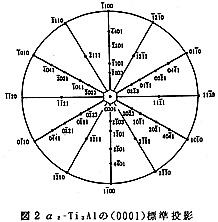
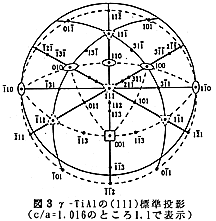
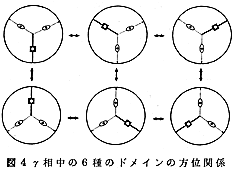
さて、ラメラ組織の形成は、α(α2)相 からγ相が板状に析出することによるが、このとき両相の間には最密面と最密方向がそれぞれ平行な結晶学的方位関係が成りたつ。その結果、結論から言えば元のα2相に対して析出するγ相はα2相の対称性のゆえに相対的には一通りであるが、γ相同志の間には6通りの方位関係があり得る。そしてこれらは、一枚のγ板の中にもドメイン(微結晶)として存在し得る。このことは、六方晶のα2-Ti3Alが積層方向の<0001>軸に関し6回回転対称であるのに対して、正方晶のγ-TiAlはc軸がa軸よりわずかに長い(c/a=1.016)ことにより、積層方向の<111>軸に関し正確に3回回転対称にならないために起こる。図2および図3には、積層面真上から見たα2とγの相対的な積層関係を示す。また図4には、図3の標準投影図の簡略図を用いてγ相中の6種のドメインの方位関係を表す。図4中のドメインは、α2の{0001}底面からγが析出する際の上下の方向によって、まず2組に分類される。これらのドメイン同志は互いに120゚回転した(オーダードドメインの)関係にあり、一枚のγ板中にも存在し得る。次に上下の異なるγ板間では、同列のドメイン同志は双晶(180゚回転)の方位関係に、その他の組み合わせは擬双晶の関係にある。したがって、γ相中の6通りのドメインはそれぞれ互いに60゚回転の関係にある。
3)γ相中の6種のドメインの分散状態
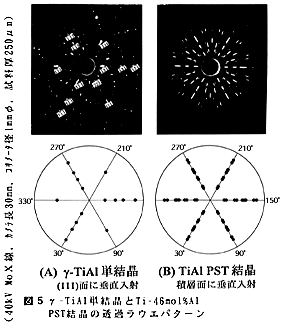 上述のとおり6通りの方位関係をもつドメインのγ相中の分散状態を知る目的で、透過ラウエ法による測定を行った。図5はγ-TiAl単結晶の(111)面、およびTi-46mol%Al PST結晶の積層面にそれぞれ平行に切り出した薄片に40kV Mo線を垂直入射して得られた透過ラウエパターンである。なお、試料の厚さは250μm、コリメータ径は1mmφとした。その結果、Ti-46mol%Al PST結晶の透過ラウエパターンは、斑点形状が放射線方向にのみ縦長となり、マクロ的には完全な六回回転対称を示した。このことは、[111] 軸を回転中心とし互いに60゚回転の関係にある6つのドメイン(γ単結晶)の回折斑点が重なって現れることにより、かつ、それらの存在確率がX線の透過域の範囲で等しいことを意味する。なお、図中下段には、γ単結晶の主要な回折斑点とそれらの重ね合わせのシミュレーション結果を示す。
上述のとおり6通りの方位関係をもつドメインのγ相中の分散状態を知る目的で、透過ラウエ法による測定を行った。図5はγ-TiAl単結晶の(111)面、およびTi-46mol%Al PST結晶の積層面にそれぞれ平行に切り出した薄片に40kV Mo線を垂直入射して得られた透過ラウエパターンである。なお、試料の厚さは250μm、コリメータ径は1mmφとした。その結果、Ti-46mol%Al PST結晶の透過ラウエパターンは、斑点形状が放射線方向にのみ縦長となり、マクロ的には完全な六回回転対称を示した。このことは、[111] 軸を回転中心とし互いに60゚回転の関係にある6つのドメイン(γ単結晶)の回折斑点が重なって現れることにより、かつ、それらの存在確率がX線の透過域の範囲で等しいことを意味する。なお、図中下段には、γ単結晶の主要な回折斑点とそれらの重ね合わせのシミュレーション結果を示す。
2.2 構成二相の単結晶の弾性定数分布とγ相中の6種のドメインの分散、積層の効果
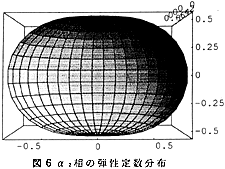
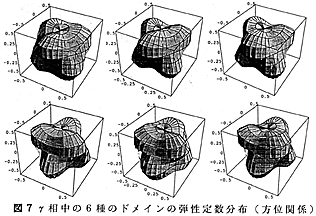
単結晶の弾性定数から回転の座標変換により任意の方向の結晶方位分布を計算、図示する方法は、前年度詳しく述べた。ここでは、三次元表示で結果のみを示す。図6にはα2単結晶の弾性定数分布を、図7にはγ相中の6種のドメイン全てについての弾性定数分布を示す。ここで言う弾性定数は正しくはヤング率の逆数にあたる弾性コンプライアンスで、単位は、10−11Pa−1である。α2相の弾性定数分布は、積層軸のまわりに回転対称の横等方性を有し、積層面については面内等方性を示す。一方、γ相は概して顕著な異方性を示す。
図7より、ドメインの弾性定数に及ぼす分散、積層の効果については、次のように考えられる。一枚のγ板中に存在する互いに120゚回転の関係にある3種のオーダードドメインは、類似の分布をとり、積層面内の異方性のみ緩和するが、γの強い異方性の緩和には概して寄与しない。しかし、この強い異方性は、γ板が積層することにより双晶の方位関係をもつドメイン同志によって打ち消される。
2.3 ラメラの巨視的な弾性的性質
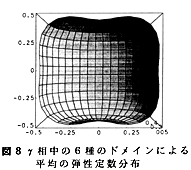
ここでは、応力一定(各相、ドメイン中の応力が不)の変仮定、いわゆるロイスモデルに依って計算を進める。計算の手順として、まず6種のドメインの存在確率が等しいとして、それらの弾性定数(ヤング率の逆数)の相加平均によりγ相の平均の弾性定数分布を求めた。図8はその結果であるが、α2相同様、横等方性を示すことがわかる。
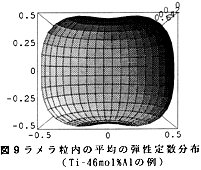
次に、ラメラ粒内の平均の弾性定数分布は、α2相とγ相の弾性定数分布に各々の相体積率を乗じて加えれば見積もることができる。そして、α2とγの層間隔やドメインのサイズ、分散状態から考えて、このようにして求めた弾性定数分布の等価な最小単位は比較的小さいものと考えられる。図9に、状態図より推察した相体積率を用いて求めたTi-46mol%Alの結果を一例として図示する。
- 結果
構成二相の単結晶の弾性的性質と積層構造に基づき、ラメラの巨視的な弾性的性質を推察することができた。今後は、圧縮試験、X線回折法等の実験的手法により検証する予定である。
最後に、本研究は金沢大学の広瀬教授のご指導のもとに行ったものである。お礼申し上げるとともに、このような展開が、現在盛んに進められているチタンアルミ合金の開発の一助になることを願うものである。
‖前のページへ戻る‖
 ラメラの積層構造を調べる目的で、試料全体が一個のラメラからなる Ti-46mol%Al PST結晶(単結晶様の結晶)を育成した。図1にその電顕組織を示す。写真はラウエ法により方位を決定した上で、正確に積層面真横から撮影したものである。これより、白く明瞭に見える薄層部分がα2相で平均の厚さは0.3μmであった。その他の部分がγ相で、強く腐食したのでγ/γ界面も見受けられ、一枚のγ板の厚さは平均約 0.6μmであった。また、一枚のγ板の中には腐食の程度に差があるドメイン(微結晶)の存在が認められる。ドメインの積層面方向のサイズは不鮮明ながら、数μmから数十μmと推察される。
ラメラの積層構造を調べる目的で、試料全体が一個のラメラからなる Ti-46mol%Al PST結晶(単結晶様の結晶)を育成した。図1にその電顕組織を示す。写真はラウエ法により方位を決定した上で、正確に積層面真横から撮影したものである。これより、白く明瞭に見える薄層部分がα2相で平均の厚さは0.3μmであった。その他の部分がγ相で、強く腐食したのでγ/γ界面も見受けられ、一枚のγ板の厚さは平均約 0.6μmであった。また、一枚のγ板の中には腐食の程度に差があるドメイン(微結晶)の存在が認められる。ドメインの積層面方向のサイズは不鮮明ながら、数μmから数十μmと推察される。


 上述のとおり6通りの方位関係をもつドメインのγ相中の分散状態を知る目的で、透過ラウエ法による測定を行った。図5はγ-TiAl単結晶の(111)面、およびTi-46mol%Al PST結晶の積層面にそれぞれ平行に切り出した薄片に40kV Mo線を垂直入射して得られた透過ラウエパターンである。なお、試料の厚さは250μm、コリメータ径は1mmφとした。その結果、Ti-46mol%Al PST結晶の透過ラウエパターンは、斑点形状が放射線方向にのみ縦長となり、マクロ的には完全な六回回転対称を示した。このことは、[111] 軸を回転中心とし互いに60゚回転の関係にある6つのドメイン(γ単結晶)の回折斑点が重なって現れることにより、かつ、それらの存在確率がX線の透過域の範囲で等しいことを意味する。なお、図中下段には、γ単結晶の主要な回折斑点とそれらの重ね合わせのシミュレーション結果を示す。
上述のとおり6通りの方位関係をもつドメインのγ相中の分散状態を知る目的で、透過ラウエ法による測定を行った。図5はγ-TiAl単結晶の(111)面、およびTi-46mol%Al PST結晶の積層面にそれぞれ平行に切り出した薄片に40kV Mo線を垂直入射して得られた透過ラウエパターンである。なお、試料の厚さは250μm、コリメータ径は1mmφとした。その結果、Ti-46mol%Al PST結晶の透過ラウエパターンは、斑点形状が放射線方向にのみ縦長となり、マクロ的には完全な六回回転対称を示した。このことは、[111] 軸を回転中心とし互いに60゚回転の関係にある6つのドメイン(γ単結晶)の回折斑点が重なって現れることにより、かつ、それらの存在確率がX線の透過域の範囲で等しいことを意味する。なお、図中下段には、γ単結晶の主要な回折斑点とそれらの重ね合わせのシミュレーション結果を示す。


