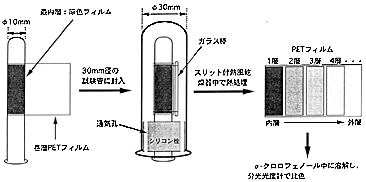
図1 拡散試験法
繊維部 沢野井康成・新保善正
2.1 実験
モデル分散染料として1-アミノアントラキノン(1-AAQ)、MC染料として1-AAQと磁性粉末をアクリル系樹脂でカプセル化したもの(平均粒子径:12.8μm)を使用した。上記の各染料をポリビニルアルコール水溶液中に均一に分散させた後フッ素樹脂フィルム上に塗布し、室温で24時間、70℃で5分間乾燥して供試原色フィルムを作製した。これを直径10mmの試験管の周囲に巻きつけ、その上にポリエチレンテレフタレート(PET)フィルム(厚さ:12.5μm)を巻層した後直径30mmの試験管内に固定し、熱風乾燥器を用いて種々の温度T(℃)でt分間熱処理した。その後、巻層したPETフィルムを展開して各層を切り取ったものをο-クロロフェノールに溶解し、分光光度計によりPETフィルム中の平均染料濃度C(mol/g)を測定した(図1参照)。

開発した装置の特長
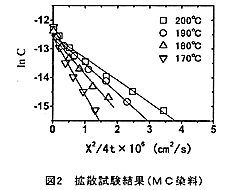
上述の方法で、170℃(21分)、180℃(16分)、190℃(12分)、200℃(8分)の熱処理をおこなったMC染料の結果を図2に示す。これから、各温度のプロットは、良好な直線関係上にあり式(3)を満足することがわかった。一方、1-AAQにおいても同様な結果がえられた。よって、今回の拡散試験法は、昇華性色素材料の拡散試験に適用可能であると考える。
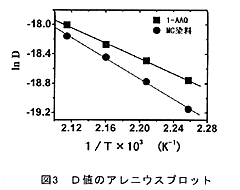
MC染料および1-AAQに関して、式(3)を用いてD値を算出し、 1/Tに対しアレニウス・プロットした結果を図3に示す。ここで、いずれも直線関係がえられた。なお、この直線部分の傾きは、拡散の活性化エネルギーΔE(kJ/mol)に比例する。したがって、MC染料と1-AAQのΔEには、特に大きな差はないものと考えられる。このことは、染料の昇華過程において、カプセル化の影響はそれほど大きくないことを示唆する。
参考文献
1)特開平9-13284
2)J.Krank,“The Mathematics of Diffusion”,2nd ED.,Chap.2(1975)